Giới thiệu
Thuật toán hồi quy tuyến tính là một phương pháp thống kê để hồi quy dữ liệu. Với biến phụ thuộc có giá trị liên tục. Trong khi các biến độc lập có thể có một trong hai giá trị liên tục hoặc là giá trị phân loại. Hồi quy tuyến tính là một trong hai dạng lớn của học có giám sát (supervised learning), dựa trên tập dữ liệu mẫu.
Nói cách khác “Thuật toán hồi quy tuyến tính” là một phương pháp để dự đoán biến phụ thuộc (Y) dựa trên giá trị của biến độc lập (X). Nó có thể được sử dụng cho các trường hợp chúng ta muốn dự đoán một số lượng liên tục. Ví dụ, dự đoán giao thông ở một cửa hàng bán lẻ, dự đoán thời gian người dùng dừng lại một trang nào đó hoặc số trang đã truy cập vào một website nào đó v.v…
Phân tích toán học thuật toán hồi quy tuyến tính
Dạng thuật toán hồi quy tuyến tính (Linear Regression)
Hồi quy tuyến tính có phương trình đạng :
F(x) = w0 + w1x1 + w2x2 + … + wnxn (1)
Trong đó, w1, w2, wn, w0 là các hằng số, w0 còn được gọi là bias hay sai số. Mối quan hệ giữa y f(x) bên trên là một mối quan hệ tuyến tính (linear). Bài toán chúng ta đang làm là một bài toán thuộc loại regression. Bài toán đi tìm các hệ số tối ưu { w1, w2, wn, w0 } chính vì vậy được gọi là bài toán Linear Regression (Hồi quy tuyến tính).
Trong phương trình (1) nếu chúng ta đặt w = [w0, w1, w2, wn]T là một vecter (cột) hệ số cần phải tối ưu và x = [1, x1, x2, xn] (đọc là x bar trong tiếng Anh) là vector (hàng) dữ liệu đầu vào mở rộng. Số 1 ở đầu được thêm vào để phép tính đơn giản hơn và thuận tiện cho việc tính toán. Khi đó, phương trình (1) có thể được viết lại dưới dạng:

Hàm mất mát của thuật toán hồi quy tuyến tính
Máy học từ giá trị trung bình của một hàm mất mát. Đây là một phương pháp đánh giá độ hiệu quả của một thuật toán nào đó trên bộ dữ liệu cho trước. Nếu kết quả dự đoán chênh lệch quá nhiều so với kết quả thực tế, hàm mất mát sẽ là một số rất lớn.
Điều tương tự xảy ra với tất cả các cặp (xi, yi), i = 1, 2, 3, …, N với N là số lượng dữ liệu quan sát được. Để hàm mất mát nhỏ nhất khi đó tổng sai số là nhỏ nhất tương đương với việc tìm w để hàm số sau đạt giá trị nhỏ nhất:
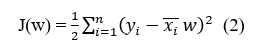
Hàm số J(w) được gọi là hàm mất mát (loss function) của bài toán Linear Regression. Chúng ta luôn mong muốn rằng sự mất mát (sai số) là nhỏ nhất, điều đó đồng nghĩa với việc tìm vector hệ số w sao cho giá trị của hàm mất mát này càng nhỏ càng tốt.
Tìm nghiệm của mô hình hồi quy tuyến tính

Mức độ lỗi của mô hình hồi quy tuyến tính
Thuật toán hồi quy tuyến tính hay bất kỳ thuật toán nào đó đều có một mức độ lỗi nhất định. Và từ mức độ lỗi ta sẽ biết được mức độ học của mô hình.

Áp dụng Linear Regression để chuẩn đoán xơ vữa động mạch
Xây dựng bộ dữ liệu với thuật toán hồi quy tuyến tính
Trong y sinh học, thường có rất nhiều yếu tố khác nhau dẫn đến một hiện tượng. Ví dụ như hiện tượng xơ vữa động mạch không chỉ do lượng cholesterol máu. Mà còn do nhiều yếu tố khác như di truyền, chủng tộc, tiền sử mắc bệnh tim mạch, tuổi, giới, BMI, tăng huyết áp, đái tháo đường,…
Trong bài viết này mình không đề cập các yếu tố di truyền, chủng tộc, giới, mắc bệnh tim mạch… mà chỉ lưu ý đến các biến số như: tuổi, cholesterol, glucose, huyết áp tâm thu và BMI. Khi đó mô hình hồi quy tuyến tính đa biến với 5 yếu tố ( x1=tuổi, x2 = cholesterol, x3 = glucose, x4 = huyết áp, x5 = BMI ) như sau:
Bề dày TM = w0 + w1(tuổi)+ w2(cholesterol) + w3(glucose) + w4(huyết áp) + w5(BMI)
Bộ dữ liệu gồm có 6 thuộc tính bao gồm: tuổi, chỉ số BMI, chỉ số huyết áp tối đa (mmHg), nồng độ glucose trong máu (mmol/l), nồng dộ cholesterol trong máu (mmol/l) và bề dày thành mạch (mm).
Bộ dữ liệu sẽ chia thành 2 phần trong đó 80% dữ liệu được làm bộ dữ liệu huấn luyện mô hình, 20% còn lại làm bộ dữ liệu thử nghiệm độ chính xác của mô hình. Dữ liệu về độ dày thành mạch làm biến mục tiêu. Những bộ dữ liệu còn lại bao gồm (tuổi, BMI, nồng độ glucose máu, nồng độ cholesterol máu) làm biến giải thích.
Note :
– Mối quan hệ giữa biến mục tiêu (Y) và biến giải thích (X) là tham số. Ví dụ Y = WX thì mỗi lần X tăng lên 1 đơn vị thì Y thêm W đơn vị dù cho bất kể X, Y có giá trị là bao nhiêu.
– Các giá trị của biến mục tiêu (Y) phải độc lập với nhau.
– Các giá trị của biến giải thích (X) không được có sai số ngẫu nhiên. Ví dụ: Giá trị huyết áp tối đa là 120 mmHg là 120 mmHg không được là 120 mmHg 2 mmHg.
#Đọc tệp
data = pd.read_csv("DuLieuYKhoa.csv", sep=";")
data.head
#In dữ liệu
print(data)
#Lấy dataframe bề dày thành mạch làm biên mục tiêu
Y = data['BEDAYTM'].to_numpy()
#Lấy datafarame không chứa bề dày thành mạch làm biến giải thích
X = data.drop("BEDAYTM", axis = 1)
#Phân loại dữ liệu train và test
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size = 20)
#Tạo model suy đoán
clf.fit(X_train, Y_train)
#In hệ số hồi quy của các biến giải thích xếp theo thứ tự tăng dần
print("\nHỆ SỐ HỒI QUY")
print(pd.DataFrame({"Tên": X_train.columns, "Hệ số":
np.abs(clf.coef_)}).sort_values(by='Hệ số'))
#In sai số
print("\nSAI SỐ")
print(clf.intercept_)
#print(clf.score())
#Tiến hành dự đoán với bộ dữ liệu test
Y_pred = clf.predict(X_test)
print("\nGIÁ TRỊ Y DỰ ĐOÁN")
print(Y_pred)
#In giá trị y test thực tế
print("\nGIÁ TRỊ Y THỰC TẾ")
print(Y_test)
#Kiểm tra mức độ lỗi của model (Mean Squared Error)
mse = sq.mean_squared_error(Y_test, Y_pred)
print("KIỂM TRA MỨC ĐỘ LỖI CỦA MÔ HÌNH")
print(mse)
Kết quả
Sau khi cài đặt thuật toán hồi quy tuyến tính và huấn luyện máy học dưới đây là kết quả:


Để cài đặt Thuật Toán Hồi Quy Tuyến Tính Chẩn Đoán Xơ Vữa Động Mạch thì các bạn download theo link dưới.
Lời kết
Thuật toán được cài đặt trên môi trường Python bằng PyCharm . Sau những gì Sharecs mong rằng sẽ giúp cho các bạn trong việc học tập cũng như tìm hiểu các thuật toán. Các bạn có thể tìm hiểu nhiều thuật toán với python tại đây.
Cảm ơn các bạn đã ghé thăm. Chúc các bạn thành công!